Estratto
Il numero di parametri, necessari per definire la configurazione di un sistema, è chiamato numero di gradi di libertà, e dipenderebbe dal sistema. Verrà mostrato che qualunque sistema può essere completamente descritto da un solo parametro.
È convinzione diffusa che, per determinare la posizione di un punto nello spazio in modo univoco, sia necessaria la conoscenza di tre numeri, le cosiddette coordinate. Possiamo scegliere vari tipi di coordinate: cartesiane, polari, cilindriche, ..., ma sempre abbiamo bisogno di tre parametri. Per questa ragione, il nostro spazio è chiamato tridimensionale. Più in generale, il numero di parametri, necessari per definire la configurazione di un sistema, è chiamato numero di gradi di libertà e dipenderebbe dal sistema.
Mostreremo qui che qualunque sistema può essere completamente descritto da un solo parametro: tutti gli elementi di R n, con n arbitrario, possono essere messi in corrispondenza biunivoca con gli elementi di un sottoinsieme di R ! (*)
Il metodo che esporremo non è l'unico possibile, ma a me pare particolarmente interessante.
Inizieremo con la posizione di un punto su un piano: i gradi di libertà sarebbero due.
Scegliamo un sistema di riferimento cartesiano sul piano, e un'unità di lunghezza u.
Chiamiamo “di ordine 0” ogni quadrato, avente i lati di lunghezza u e paralleli agli assi.
Ogni quadrato di ordine 0 può essere diviso in 9 quadrati più piccoli, che numeriamo come in fig. 1a. Chiamiamo questi quadrati “di ordine −1”, e il numero associato a ciascuno, il suo “coefficiente”.
La suddivisione può continuare (fig. 1b), formando quadrati sempre più piccoli. Chiamiamo “di ordine k − 1” i quadrati ottenuti dividendo un quadrato di ordine k, e li numeriamo come in precedenza.
Analogamente, congiungendo 9 quadrati di ordine k, possiamo costruire un quadrato più grande, che chiamiamo “di ordine k + 1” (fig. 1c).
Per determinare la coordinata unica (ξ) di un punto, costruiamo il quadrato di ordine minore, centrato nell'origine e contenente il punto (assumiamo che un punto è contenuto in un quadrato, anche se si trova sul suo perimetro). Sia k l'ordine di questo quadrato. Lo suddividiamo e determiniamo il quadrato, di ordine k − 1, che contiene il punto. Sia c k − 1 il suo coefficiente. Se il punto si trova sul confine tra più quadrati, possiamo fissare una convenzione arbitraria. Per esempio, possiamo scegliere il quadrato col coefficiente più basso.
Continuiamo la suddivisione, ottenendo quadrati sempre più piccoli, che contengono il punto. c i è il coefficiente del quadrato di ordine i contenente il punto.
Infine, poniamo
Ciò è equivalente a scrivere un numero in base 9, dove i c i sono le cifre.
In fig. 2 è mostrato un esempio: il quadrato più grande, centrato nell'origine, è di ordine 1; il coefficiente del quadrato di ordine 0, contenente il punto, è 3; il coefficiente del quadrato analogo di ordine −1 è 7; quello del quadrato di ordine −2 è 8. Arrestando qui il procedimento, possiamo scrivere
ξ = (3,78) 9 ≈ 3,88
Questo grado di approssimazione localizza il punto in un quadrato di area 1 / 9 2 u 2. Se fissassimo tutte le infinite cifre del numero in base 9, determineremmo la posizione del punto esattamente e in modo univoco.
Per ricordare che l'unità di lunghezza è u, possiamo esprimere la coordinata nella forma
ξ = 3,88 u × u
che può adattarsi anche al caso di unità diverse per i due assi.
La generalizzazione a n dimensioni, o, equivalentemente, a n gradi di libertà, è immediata. Basterà sostituire i quadrati con degli ipercubi n-dimensionali, dividerli non in 9, ma in 3 n parti, numerare queste ultime secondo una data convenzione (avendo cura che il coefficiente dell'ipercubo centrale sia 0), e scrivere un numero non in base 9, ma in base 3 n.
Per mezzo della coordinata unica possiamo descrivere l'evoluzione di un sistema mediante una sola equazione. Per esempio, per il moto di un punto materiale nello spazio, anzichè tre equazioni, possiamo scrivere formalmente
O ξ (t) = f
dove t è il tempo, f è la forza, per unità di massa, espressa mediante un solo parametro, e O è un operatore non lineare. Sfortunatamente, è molto difficile esprimere questa equazione esplicitamente e risolverla, ma il problema è interessante.
Ho studiato il comportamento di ξ (t) nel caso particolare di un moto rettilineo uniforme in un piano. La funzione ξ (t) è fortemente discontinua, e il suo grafico presenta una struttura frattale. Il caso y = 0, x = t (velocità unitaria) è mostrato in fig. 3.
(*) Dopo aver terminato questo scritto, ho imparato che il fatto, che R n abbia la stessa potenza di R, era già stato enunciato da Cantor nei suoi lavori sui numeri transfiniti.
NOTA DEL 13/03/2005. Se un punto si trova in un vertice, la sua coordinata unica, scritta in base 9, può avere, da un certo punto in poi, tutte le cifre uguali a 8, ad esempio (0,888...) 9 . Ma (0,888...) 9 = (1,000...) 9 , che è la coordinata di un altro punto.
Si può risolvere questo problema modificando le convenzioni proposte nel testo. Basta ad esempio assumere che ogni quadrato non contenga tutti i punti del suo perimetro, ma resti escluso il vertice in alto a sinistra. In questo modo, (0,888...) 9 verrebbe sostituito da (1,666...) 9 .
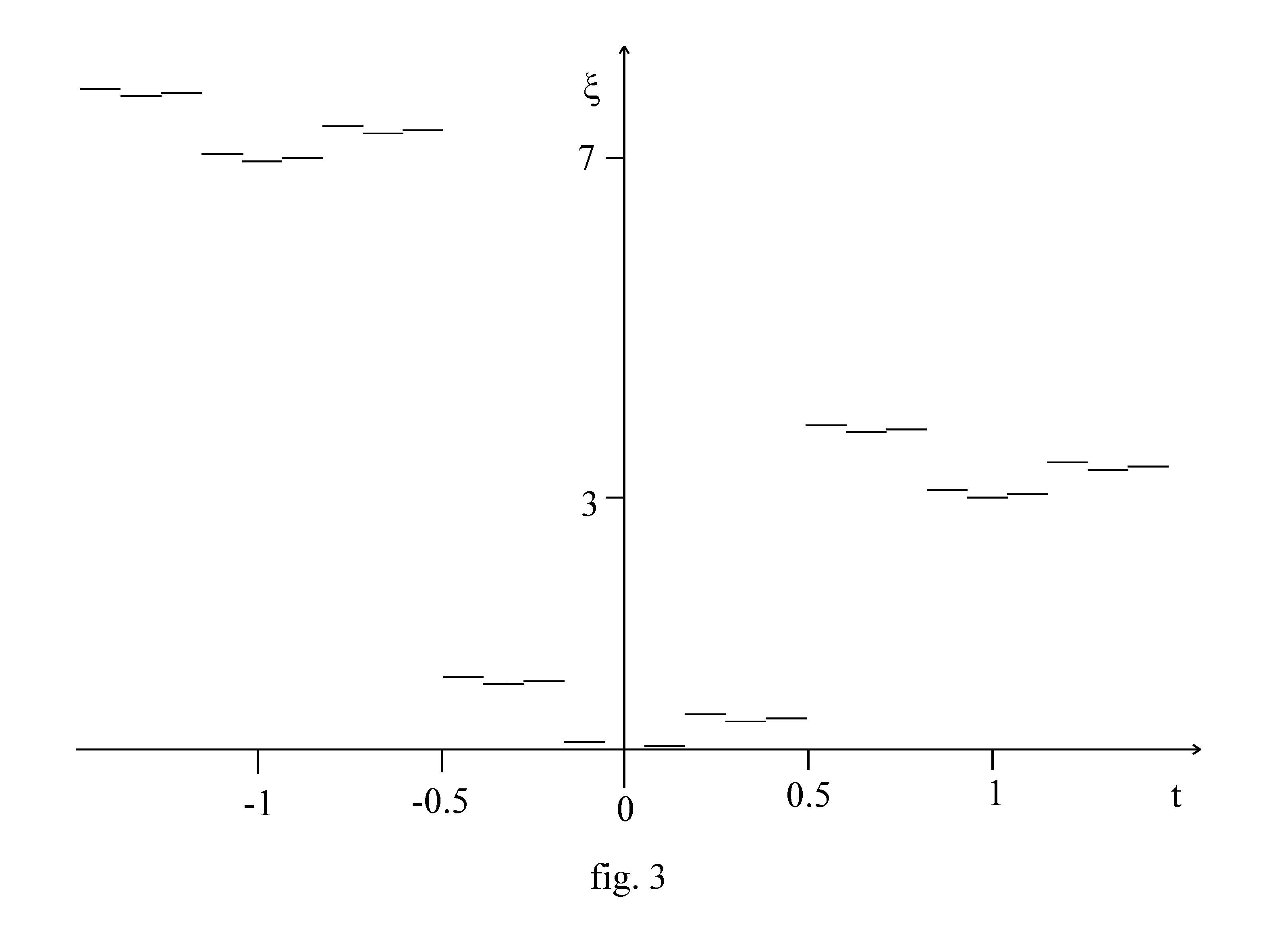
(per stampare questo grafico, selezionarlo e stamparlo orizzontalmente)