Abstract
The number of parameters, necessary to define the configuration of a system, is called number of degrees of freedom, and it would depend upon the system. We show that any system may be completely described by a single parameter.
It is a diffuse conviction that the knowledge of three numbers, the so-called co-ordinates, is necessary to determine the position of a point in the space in an univocal way. We can choose various types of co-ordinates: the Cartesian ones, the polar ones, the cylindrical ones, ..., but always we need three parameters. For this reason, our space is called three-dimensional. In more generality, the number of parameters, necessary to define the configuration of a system, is called number of degrees of freedom, and it would depend upon the system.
Here, we shall show that any system may be completely described by a single parameter: all the elements of R n, with arbitrary n, may be put in biunique correspondence with the elements of a subset of R ! (*)
The method, that we shall expose, is not the only one, but I think it is particularly interesting.
We begin with the position of a point on a plane: the degrees of freedom would be two.
We choose a Cartesian reference frame on the plane, and a unit of length u.
We call “of order 0” every square, having its sides u long and parallel to the axes.
Every square of order 0 may be divided in 9 more small squares, that we number as in fig. 1a. We call these squares “of order −1”, and the number associated to each one, its “coefficient”.
The subdivision may continue (fig. 1b), forming more and more small squares. We call “of order k − 1” the squares obtained dividing a square of order k, and we number them as previously.
Analogously, joining 9 square of order k, we can construct a greater square, that we call “of order k + 1” (fig. 1c).
In order to determine the single co-ordinate (ξ) of a point, we construct the square of the least order, centred in the origin and containing the point (we assume that a point is contained in a square, also if it is on the perimeter). Let k be the order of this square. We subdivide it and we determine the square, of order k − 1, containing the point. Let c k − 1 be its coefficient. If the point is on the border between different squares, we can fix an arbitrary convention. For example, we can choose the square with the least coefficient.
We continue the subdivision, obtaining more and more small squares, that contain the point. c i is the coefficient of the square of order i containing the point.
Finally, we put
This is equivalent to write a number in base 9, where the c i are the figures.
In fig. 2 an example is shown: the greatest square, centred in the origin, is of order 1; the coefficient of the square of order 0, containing the point, is 3; the coefficient of the analogous square of order −1 is 7; the one of the square of order −2 is 8. Stopping here the proceeding, we can write
ξ = (3.78) 9 ≈ 3.88
This degree of approximation localises the point in a square of area 1 / 9 2 u 2. If we fixed all the infinite figures of the number in base 9, we should determine the position of the point exactly and in an univocal way.
In order to remember that the unit of length is u, we can express the co-ordinate in the form
ξ = 3.88 u × u
that may fit also the case of different units for the two axes.
The generalisation to n dimensions, or, equivalently, to n degrees of freedom, is immediate. It will be enough to replace the squares with some n-dimensional hyper-cubes, to divide them not in 9, but in 3 n parts, to number these according to a given convention (taking care that the coefficient of the central hyper-cube be 0), and to write a number not in base 9, but in base 3 n.
By means of the single co-ordinate we can describe the evolution of a system by a single equation. For example, for the motion of a point mass in the space, rather than three equations, we can write formally
O ξ (t) = f
where t is the time, f is the force, per unit mass, expressed by a single parameter, and O is a non-linear operator. Unfortunately, it is very difficult to express this equation explicitly and to solve it, but the problem is interesting.
I have studied the behaviour of ξ (t) in the particular case of a uniform straight motion in a plane. The function ξ (t) is strongly discontinuous, and its graph presents a fractal structure. The case y = 0, x = t (unitary velocity) is shown in fig. 3.
(*) After having finished this paper, I have learned that the fact, that R n has the same power of R, had been already enunciated by Cantor in his works on the transfinite numbers.
NOTE OF 13/03/2005. If a point is in a vertex, all the figures of its single co-ordinate (in base 9) may be 8, from a certain point forward, for example (0.888...) 9 . But (0.888...) 9 = (1.000...) 9 that is the co-ordinate of another point.
We can solve this problem, modifying the conventions proposed in the text. For example, it is sufficient to assume every square not to contain all the points of its perimeter, but the vertex on high on the left to be excluded. In this way, (0.888...) 9 would be replaced by (1.666...) 9 .
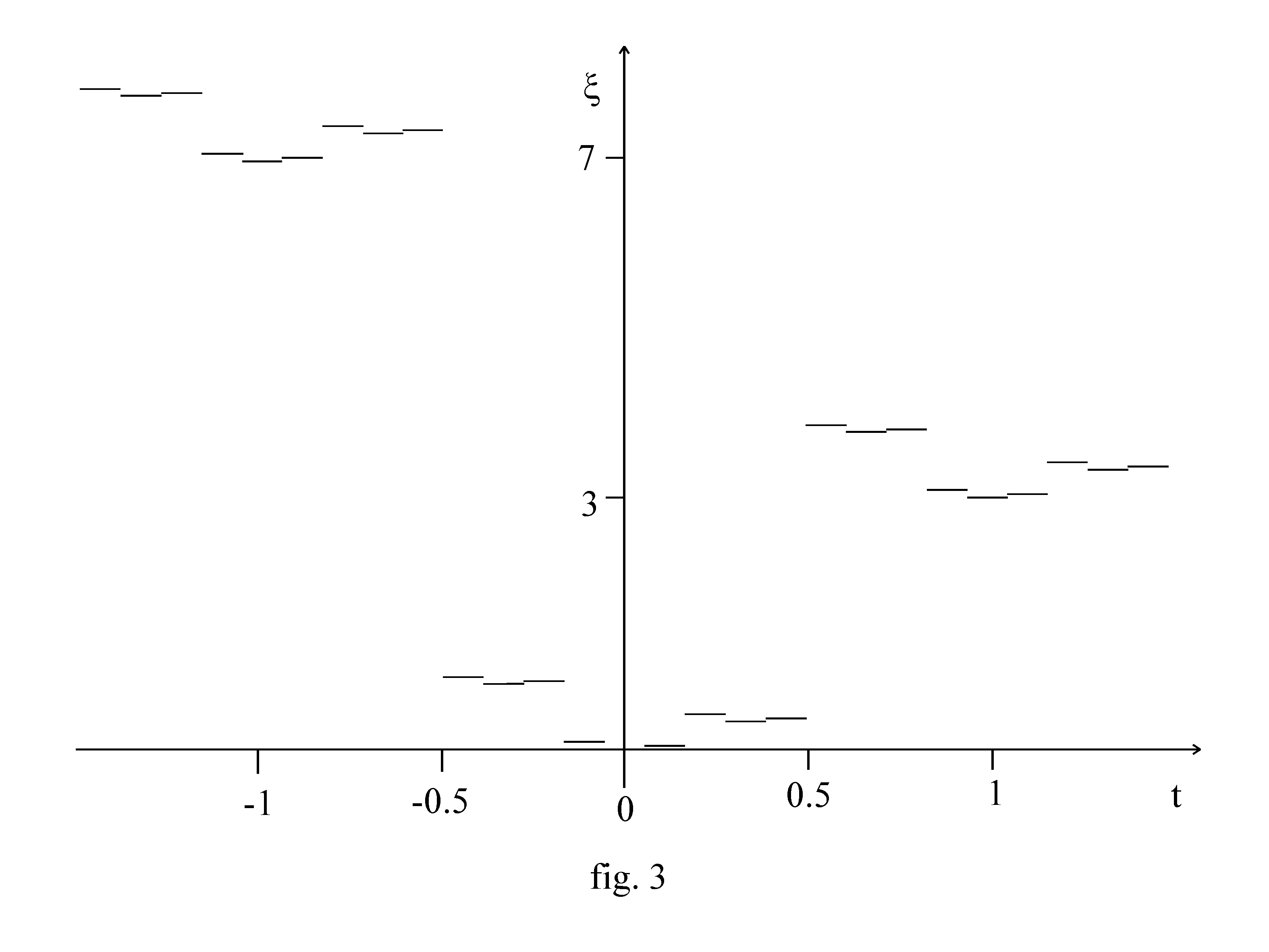
(in order to print this graph, select it and print horizontally)